ColorAC のテクノロジー
記事の順番を、新しい記事を後に追加する時系列にしていましたが、新しい記事が上に来る様に 逆にしました。(ブログなどと同じにしました)
目次:
記事の順番を、新しい記事を後に追加する時系列にしていましたが、新しい記事が上に来る様に 逆にしました。(ブログなどと同じにしました)
ColorACでICCプロファイルからデータをインポートする際に、クリップの可能性についての警告が出る場合があります。これについて解説してみます。
ICCプロファイルは、色域の異なるプロファイル(特性)の間でデータをやり取りするために、色度をPCS(Profile Connection Spaces)と呼ぶ共通のデータフォーマットに変換します。 PCSは通常、CIEのXYZを元にした形式(PCSXYZ)またはCIEのLab(CIE 1976 L*a*b*)を元にした形式(PCSLAB)のどちらかを使います。また、プロファイルの特性を記録したTagのデータ形式は、都度のデータ形式変換を避けるためにPCSに合わせた形式て格納されます。
この2つのPCSの形式の中で、一般に色彩の振る舞いを表現するにはPCSLABが優れているとされるので、ICCプロファイルを作成する時は、PCSLABが採用されるケースが多い様です。
ただ、PCSLABは、a*とb*の範囲が-128~127に限定されています。これを超える色は表現できません。(より詳細には、ICCプロファイルのバージョンやタグにより多少扱いが異なります。Ver4.2のPCSLABは+127が最大値。)
-128~127の範囲がどの程度の広さかと言うと、およそAdobeRGB(D50に色順応変換した)が表現できる程度の範囲です。特にそのG(緑)原色点は およそa*=-129とほぼ限界に等しい数字になっています。
AdobeRGBは、一般に使われているディスプレイとしては広色域ですが、今時はAdobeRGBを超えるディスプレイもあるし、AdobeRGB色度準拠のディスプレイでも、製品のバラツキで 実際の色度がAdobeRGB色域よりも外側にずれている可能性もあります。その場合は、先のL*a*b*形式の範囲では特性を表現しきれなくなります。
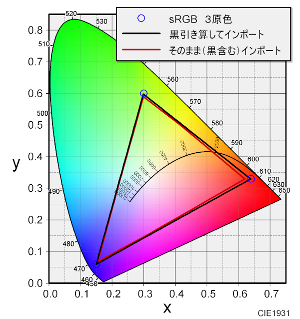
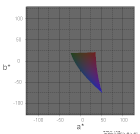
例として、Greenの原色の色度がAdobeRGBよりも濃い場合について、どうなるか見てみます。下図にWideGamutと言う名前で、 AdobeRGBよりも広い色域の例を xy座標で示しました。
これがICCプロファイル内でどう表現されるかを考えるため、D50に変換して、a*b*の範囲を見ると次の図の 赤線で示した128Limit(D50) の様になると考えられます。-128の外に出た部分が、切り取られて無くなった様な形です。
この-128で切り取られた形状の128Limit(D50)を xy座標上に戻すと下図の様になります。Gの原色の部分が欠けている様に見えます。
以上の現象は、ICCプロファイルを作成する条件として、PCSをXYZに指定する事で一旦は解決します。
ただ、XYZの形式よりもLab形式の方が特性モデルとして精度が良い(中間調の時の補間精度が良い)ので、PCSとしてXYZを選択すると補間精度の低下と言う欠点が出ます。 PCSをLabにしたまま、クリップ現象を起こさせない方法があるかどうかについてですが、残念ながら私は知りません。
ColorACでICCプロファイルから色度データをインポートする時、かなり大雑把な方法ですが、PCSがLAB形式で かつ a*,b*が±128に近いデータになっている場合には、警告を出す様にしています。
この警告は、ディスプレイの表示特性に異常があると言う意味ではなく、ICCプロファイルに書き込まれたデータの内容に関するものです。
上記の例の様にGの色度点が多少クリップしている程度であれば、カラーマネージメントと言う意味では、Gの強度が強い部分だけに影響が出るので、ほとんど問題にならないのかもしれません。 ただし、ICCプロファイルを使ってディスプレイの色域を評価する場合には、注意が必要です。
警告が出た場合は、CIELAB形式で色域をインポートして、*a,*bの値が飽和していないか確認してみてください。
ディスプレイがどれだけ広い範囲の色彩が表現できるかを示す 色域(Color Gamut)の表現方法として、 簡便な "色度図上の面積で表現する" 方法が、良く使われます。 特に "NTSC比”に代表される様に、広く知られている色域(たとえばNTSC1953とかsRGBなど)を基準にした面積比で表現する方法が 良く用いられています。
ColorACでも、もちろんこの計算ができます。操作方法と注意点を記載しておきます。
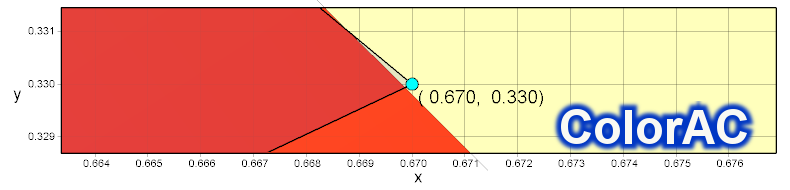
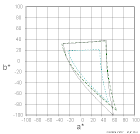
RGBWアイテムや多点アイテムで RGBの3原色の色度を入力している場合は、 3原色の色度点が作る三角形の面積を色域として計算します。 NTSC比であれば、特に指定しなくてもサマリに表示されます。
たとえばRGBWアイテムにRGB色度を入力した下図の例では、色度図とサマリは次の様になります。 xy座標における面積は0.093でNTSC比は58.9% 、u'v'では面積0.050、NTSC比67.5% となりました。
このRGBWアイテムを使う方法では、情報としては3点の座標のみで、色域は三角形の面積として色域が計算されます。 NTSC比のNTSCとは、1953年に制定された古いNTSCの規格に含まれるTV用の色度規格で
3原色の座標は
| Color | x | y |
|---|---|---|
| R | 0.670 | 0.330 |
| G | 0.210 | 0.710 |
| B | 0.140 | 0.080 |
となっています。(この色度は、RGBWアイテムのプリセットデータにもあります)
こ3原色の色度が作る三角形の面積(CIE1931xyでは 0.1582)との比率がNTSC比です。
他の色域(上記のNTSCではない)を基準とした比率の数字が欲しい時は、領域重なりアイテムを使って計算します。カバー率が欲しい時も領域重なりアイテムで計算できます。
表示アイテイムの構成は次の様になります。
たとえば、sRGBの3原色と上記のデータを比べてみます。sRGBの3原色を多点アイテムに入れて、 領域重なりアイテムのサマリを見ると次の様になっています。、
また、計算結果はアイテムリスト上にも表示されています。黒背景文字の部分がカバー率です。
ColorACは、データ補正アイテムを使ってRGBの原色に加えて、黒のXYZを入れる事ができます。 この黒を使って たとえばディスプレイのわずかな光漏れや、ディスプレイに外光が当たって、 表示が白っぽくなってしまっている状況(コントラスト低下)等を表現する事を想定しています。
注意として、黒の明るさが入ると、色域は 必ずしも3角形ではなくなります。 ColorACのデータ補正アイテムの黒の扱いは、RGBの表示強度に係わらず一定のXYZが表示されている想定で、 この場合は、色域は6角形になります。色域は単純に3角形で計算した場合よりも少し広くなります。
ColorACは、正しく多角形の面積として色域を計算します。しかし色域の計算方法が”3原色の座標が作る三角形の面積”と明確に指定されている場合があるので、注意が必要です。
その場合はColorACで、データ補正アイテムを使って計算すると数値が合わなくなります。 (三角形の面積で計算したい場合は、3原色の数字を直接指定する(1)の方法で実施してください)
ICCプロファイルは、上記(2)の黒を入れた単純なモデルよりも、より複雑で詳細な表示特性のモデルが使えます。どのモデルを採用して、パラメータに何の数値を入れるか、プロファイルを作る側の裁量が大きく、 色域計算に使った時の結果の解釈にも注意が必要です。
また、ICCプロファイルの中でCIELAB形式を使っている場合は色域が制限されるので、広色域の検討では制限に掛かっていないかどうかにも注意が必要です。
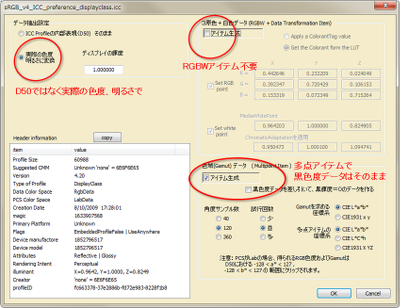
ColorACでICCプロファイルからデータをインポートする時に、ColorAC側のデータ形式として2つ準備しています。
評価対象のディスプレイの色域(Gamut)を得るためにインポートする時は、多点アイテムでインポートする事を推奨します。 これは、ICCプロファイル側で採用したモデルの種類によらずに正しく色域を計算した結果が得られるためです。
インポートのダイアログ画面の設定は、初期設定(default)のままで良いです。データ抽出設定として 「実際の色度 明るさに変換」になります。 また、「黒色度データを差し引いて、黒輝度=0のデータを作る」は非選択のままにします。
これで、実際のディスプレイを評価したデータに相当する色度を取り込む事ができます
色域をインポートした後の扱いは、既に記載した領域重なりアイテムで計算する方法が使えます。領域重なりアイテムは 多角形の面積、多角形同士の重なり面積の計算に対応しているので、多点アイテム形式で問題ありません。
ICCプロファイルを活用する時、もう一つ重要な注意点があります。
基準の色域をICCプロファイルからインポートする場合は 上記 評価対象のICCプロファイルの扱いとは全く逆の考え方が必要になります。 多くの場合、余計な黒輝度を含まない規格通り(理想値)の原色の色度を得るためには、黒を差し引いて読み込む事が必要です。
”多くの場合”と推測になるのは、基準に使うICCプロファイルの作り方に依存しているからです。 ICCが提供しているsRGBのICCプロファイルや、Adobeが作成したAdobeRGBのICCプロファイルを確認した限りでは、
規定の色域に黒輝度を加えて色域が狭くなった状態のプロファイルの作りになっています。 この様なICCプロファイルから規格の色度を得るには、黒輝度を差し引く事が必要になります。
( 黒輝度=0の設定になっているICCプロファイルも多いです。その場合は黒の差引は不要ですし、ColorACのインポート設定画面上でも黒輝度を差し引く選択ができない状態になります。AdobeRGBのICCプロファイルは、黒輝度=0でした。訂正しました。)
ICCが公開しているsRGBのICCプロファイル(Ver 4.2)から色域を読み込んだ例を示します。
基準の原色色度の座標が分っている場合には、ICCプロファイルから基準色域のデータを引き出すのは避けて、直接RGBWアイテムに数値を入力して基準を作った方が確実です。 また、NTSCやAdobeRGB,sRGBに対する比率が必要な場合は、ColorACに座標データがプリセットされているので、それを活用すると簡単です。
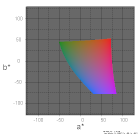
CIE L*a*b*(CIELAB)の2次元図a*-b*や、a*-b*の断面形状(3D)の図は 良く見かける色度図のひとつです。
ColorACでも、RGBの3原色の色度(RGBWアイテムを利用)からa*-b*の色域図を簡単に描く事ができます。このサイトのギャラリーにも sRGBなどのa*-b*色域図を掲載しています。
しかし、このColorACで描いた色域図と、ネット上で見かける色域図とが少し違っている場合がある(と言うよりも、違う色域図が多い)事に気づいた方もいるでしょう。
この状況から、ColorACで描画した図が間違っていると思った方もいるかもしれません。 この誤解を解くために、ネットで良く見る図とColorACの図で何が違うのか、WikipediaのLab色空間のページに掲載(2015年7月時点)のa*-b*色度図を例に確認、説明してみます。
WikipediaのLab色空間のページに、sRGBのL*固定のa*-b*図が掲載されています。 この図です(WikipediaのLab色空間のページの画像データをリンク)。

この図には「sRGBの色域に収まる範囲(一般的なコンピュータのディスプレイに表示できる範囲)」と説明が付いています。 この説明を見る限りsRGBとは ごく一般的な解釈、以下の色度、またはそれを元にしたものを指していると言う事で間違いないと思われます。
| Color | x | y |
|---|---|---|
| R | 0.640 | 0.330 |
| G | 0.300 | 0.600 |
| B | 0.150 | 0.060 |
| W | 0.31271 | 0.32902 |
ところが、ColorACでこの色度を使って、Wikipedia掲載の図と同じL*固定の図を描いてみても 形状が一致しません。何が違うのでしょうか?
もったいぶらずに結論を書いてしまうと、Wikipedia掲載の図は、プロットするsRGBの色度点を、D50の白色基準に変換(色順応変換)した上で、L*a*b*でプロットしている様です。
これは推定にすぎませんが、以下の様にいくつかの条件で色度図を描いて比較してみた結果、D50に変換する事でWikipedia掲載の図と良く似た図が描ける事が確認できました。
実は、グラフの範囲が-128~128と言う2進数を想起させる数字を適用している点だけでも、この図の由来が推定されます。この"128"については また別の記事を書くつもりです。
Wikipedia掲載の図はsRGBであり、かつ、なぜか違う色度図になっている。比較しているColorACの色度図は、単純にsRGBの原色の色度に基いてa*-b*を描いていますが、これにディスプレイの表示条件を追加すると、色度図が変わってきます。
Wikipediaの図では、どんな条件を付与したのか。まず考えられるのが、黒表示レベルを追加する事で色域が変化している場合です。 実際のPCモニタの使用環境では外界の写り込みなどがありますし、たとえそれが無かったとしても、ディスプレイの特性のため完全な黒の表示はできません。この黒はRGB単色の表示にも影響を与えるので、色域が変化します。
たとえばICCが作ったsRGBのICCプロファイルの表示色を確認すると、上の表の3原色とは違う色域になっています。それは黒輝度(Black point)が設定されているためです。黒輝度を考慮したL*固定図を描いてみると、以下の様になります。
黒が明るくなる要因は複数あり各種条件に依存します。sRGBをの規定を調べても黒の明るさを一意に決める事ができないので、ここでは例としてICCプロファイルに入っていた黒を使っています。 また、黒による変化の様子が分りやすくなる様にICCプロファイルに入っている黒の10倍の明るさの黒を適用した場合も表に入れてみました。
まず、xy色度図で見ると、この様になっています。
この3つのディスプレイをL*一定のa*-b*図に描くと、下表の様になります。(a*-b*図の画像データを作成する時のRGBの値は黒輝度=0の理想的なsRGBのディスプレイに表示する想定で計算しています)
Wikipedia掲載図の利用承認を取る手間を避けるため、この表にはWidipediaの図は掲載していません。その代り右端に色域形状の比較図を追加しました。形状比較図は見易い様に拡大して±100の範囲の表示にしています。
| 色度図で表現するディスプレイ | sRGB+黒Y=0 | sRGB+黒Y=0.0125 | sRGB+黒Y=0.125 | Wikipedia図と比較 |
|---|---|---|---|---|
| 色度図画像をレンダリングする色空間 | sRGB (白色=D65,黒Y=0) | |||
| L*=75 | 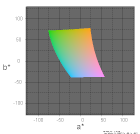 |
 |
 |
 |
| L*=50 | 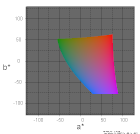 |
 |
 |
 |
| L*=25 | 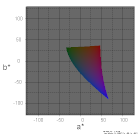 |
 |
 |
 |
黒の数字(黒の明るさ)を入れる事で、L*一定で描画できる色の範囲は減ります。”sRGB+黒Y=0.125”の場合は、Y=0.125の黒だけで 明るさL*=25を超えるため L*=25の図は空になっています。
これらColorACで描いた図とWikipediaに掲載の図を比べてみると、色域の広さと言うよりも、形状が違っています。黒レベルを調整して 色域の大きさを調整しても ColorACの結果とWikipedia掲載の図が一致する事はありません。 色度図の不一致は、想定する黒レベル条件の差が原因と言う事では無さそうです。そこで黒ではなく別の要因の可能性を考えます。
次に考えたのは、色順応などの観察者側の要因を入れて、sRGBの色度から他の色度に変換してしまっている場合です。sRGBの白色はD65ですが、これとD50を組み合わせてみます。 以下、sRGBのRGBと白色をD65からD50への色順応変換を施したものをsRGB(D50)と表記します。色順応変換の手法は、ICCで良く使われるBradford Transformです。
xy色度図で見ると、この様になっています。
この2つのディスプレイをL*一定のa*-b*図に描くと、下表の様になります。
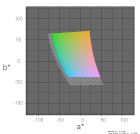
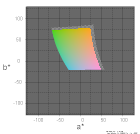
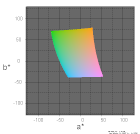
| L*a*b*の白色基準 | D65 | D50 | D65 | D50 |
|---|---|---|---|---|
| 色度図で表現するディスプレイ | sRGB | sRGB(D50) | ||
| 色度図画像をレンダリングする色空間 | sRGB | sRGB(D50) | ||
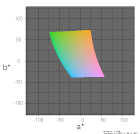
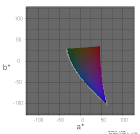
| L*=75 | 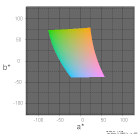 |
 |
 |
 |
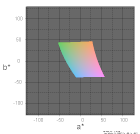
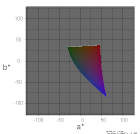
| L*=50 | 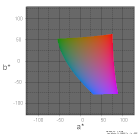 |
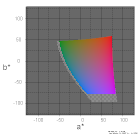 |
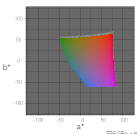 |
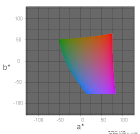 |
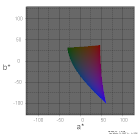
| L*=25 | 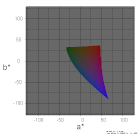 |
 |
 |
 |
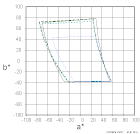
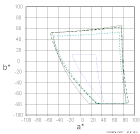
黒レベルを入れた時と同様に、図を見比べただけではWikipediaの図との比較が難しいので、以下に形状比較を示します。
ColorACでsRGB(D50)をD50基準で描画した図と Wikipediaの図が良く一致している事が分ります。 (Wikipediaの色域図の形状は、掲載の画像から読み取って作ったため、あまり精度が良くありません)
WikipediaのsRGBの色度図は、sRGBをD50に色順応変換してから描画して作ったと考えられます。
突然D50と言う標準光源の名称が出てきましたが、sRGBの色度をD50の白色基準に変換する事はどんな意味があるのでしょうか?なぜD50なのでしょうか。
私がD50への変換に関連していると推測したのは、D50に色順応変換してから描いた色度図を、とても良く使っているグループがいるからです。 それはカラーマネージメントのコミュニティです。
ICCでのカラーマネージメントにおける表示データの色域変換の計算は、一旦、カラーマネージメントの対象デバイスの色域(色空間)をD50基準に変換してから、変換を実施する手順です。 色域変換した後に変換先デバイスの白色基準(sRGBであればD65)に戻して変換結果を使います。これがD50に色順応変換した色度を使う理由の様です。
もっとも、これは色度図を描く手順ではありません。あくまでカラーマネージメントのためのデータ処理の途中にD50に変換したデータを扱う段階があると言う事ですが、 色域変換に使うL*a*b*のデータをそのまま表示すると、D50基準のL*a*b*図になっている訳です。
ICCプロファイルなどのカラーマネージメントシステムの実装としては、D50に変換後の形式でデータを保持しているため、自然とD50基準のL*a*b*図になります。
このカラーマネージメントのプロセスは、異なる照明環境、あるいは別の白色基準のデバイスでの色の見え方を比較、変換するために実行される処理です。L*a*b*の形式よりも色順応変換の方が主役です。 L*a*b*の形式で色を表現する事は、多くの場合計算精度を上げる工夫にすぎません(実際、規格化された三刺激値も使われています)。また、共通の環境としてD50が選ばれるのは、主に歴史的な経緯によるものです。
従って、L*a*b*の表示のためにD50に変換すると言うのでは本末転倒ですが、カラーマネージメントに関連する場合ば問題無いでしょう。
では、この表示デバイスの色度をD50に変換して扱うと言う方法が、カラーマネージメントやそれ以外も含めてどんな場面でも常に適切かと言う事になると、さすがにそれは違います。世の中にD50ではない環境、デバイスが沢山あります。ディスプレイの白色とD50の間で変換すれば万事解決ではありません。そもそも、色順応とL*a*b*は別のものです。
このD50に変換する方法にメリットがあるのは、想定する白色の色度の色順応計算が有効な場面に限定されます。素直にL*a*b*を計算した方が良い場面も多いはずです。
L*a*b*の使い方として、D50に変換して扱う事では うまくいかない例をひとつ挙げます。 前のCIE2000色差の計算に書いた、D65のモニタと7000Kのモニタの色比較の様な場面です。
ここでは色の差が目視しやすい様に7000KではなくD93(およそ9300K)を例にします。色域もモニタで見やすい様にAdobeRGBではなくsRGBを想定します。
これが、sRGB用のカラーパッチをD65とD93のディスプレイに表示したイメージのビットマップです(右側がD93です)。
注意:比較しやすい様に、カラーパッチの周辺はL128のグレイに統一しています。また、D93ディスプレイ前提では、色がsRGB色域の外にはみ出てしまうので、ビットマップのRGB値は 単純に0~255の範囲に丸めてしまっています。正確な変換とは言えません。以下のD50への変換した場合等も同様です。
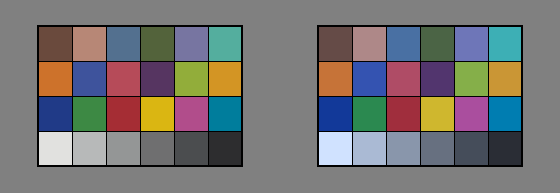
当然ですが、明らかに色が違って見えます。D65と比べてD93は 青っぽくなっているのが分ると思います。これほどはっきりわかる例ですので、色差をそのまま計算すれば、大きな数字になりす。
では、それぞれの表示を 先ほどの「モニタの白色をD50に変換する」と言うプロセスを実施してみます。・・・理屈からして計算するまでも無いですが。
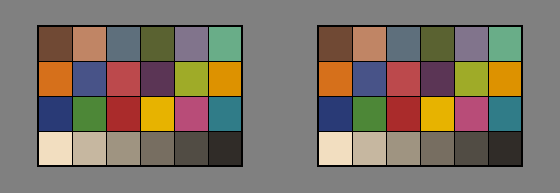
D50に揃えてしまった訳ですから、両者は同じ色になりました。
この状態のL*a*b*の値で色差を計算したらどうなるでしょうか。当然色差はありません。色順応の変換の意味を理解せず、盲目的にD50に変換すると、D65のモニタの表示とD95のモニタの表示に色差は無いと言う結論になってしまいます。これは一般には間違と言って良いでしょう。
「色順応したらD65のモニタとD93のモニタに差は無いから、色差は無いと言う結論は正しい」と言う意見もあると思います。 それこそ「色順応したら」ですから、その様な前提が成り立つ場面でのみ適用できます。 前のCIE2000色差の計算では、色差を計算する前提としてD65のモニタと7000Kのモニタを並べて見て比較していると状況では成り立ちません。
以上は極端な例ですが、ここまで酷くないにしても、意味を理解せずにD50に変換すると、目的に沿わない結果が得られる場合がある事が分ると思います。
以上の様に、ColorACのL*a*b*図の描画が間違っている訳ではないです。
D50に変換した色度図を描画したい場合は、その様にデータを作る必要があります。ColorACは汎用を主眼に作っているため、ディスプレイの色度図を描く条件は、前提とする環境条件など複数あるため、目的の条件を設定する必要があると言う事です。
ただ、確かにD50に変換した色度図は利用頻度が高いかもしれないので、要望がありましたら、もっと手間が省ける選択枝を追加しても良いかもしれません。
ICCプロファイルからのインポートを使う場合に、D50のままインポートして色度図を作成すればD50の図が作れます。
WikipediaのL*a*b*のページにはICCやAdobePhotoshopなどでD50基準で取り扱っていると言う様な記載や「絶対的値を示すレンダリングインテントである ICC L*a*b* はCIE標準光源 D50 をホワイトポイントとした・・・」と書いているので、 筆者はD50に変換して取り扱う事が「ある分野に限定された手法」である事を認識しているはずですが、 D50に変換した状態の色度図だけを、この変換に関する説明は全く無く掲載しています。
一方で特記しておきながら、色度図の例には解説無しでの適用は不釣り合いなので、せめて注釈は欲しいですね。
先ほどの例で、D50への変換について D65とD95のデータを一括してD50に変換すれば、色差を残したままD50に変換する事ができるし、そうすべきと言う反論が考えられます。
ではやってみます。D65とD95の平均値からD50への変換を両方に掛けてみました。
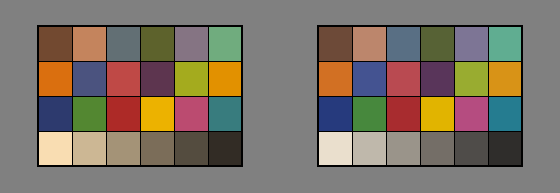
これならば確かに色差は残ります。D50の環境に変換する必要がある場合であれば、有効かもしれません。 これは、色順応計算は環境を正しく見て設定する必要があると言う例にはなります。
現在 信頼できる色差式としてCIE 2000色差式(以下dE2000)の採用が推奨される場面が増えてきました。
ColorACにもdE2000が実装されていますが、dE2000の計算式は少々複雑なので、注意して計算式をプログラムに変換する必要があります。そこでColorACでの計算の確認結果と、適用例を挙げてみます。
色差式を実装した時、最初は他のdE2000の計算手段と比較するのが早いと考え、ネット上にいくつかある dE2000色差計算のコンテンツに データを入れて、計算結果を比較しようとしました。 しかし、そもそもコンテンツの間でも計算結果が合わない事が分り、どれが正しいか分からないので検証に使うのは諦めました。
リファレンスになりそうな報告書を探したところ、うってつけの文献が見つかりました。 "The CIEDE2000 Color-Difference Formula: Implementation Notes, Supplementary Test Data, and Mathematical Observations," です。いろいろな条件のデータが網羅され、色差値も掲載されています。また、整理された計算式も掲載されていて、大変参考になります。
この文献のテストデータを使って、ColorACが文献の色差計算結果を再現できるかやってみました。
次表が結果です。表の右端の誤差とは、この論文記載の色差値を正として、それに対しての差です。
| Data No. | L1 | a1 | b1 | L2 | a2 | b2 | 文献のdE2000 | ColorACによるdE2000 | error |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 2.6772 | -79.7751 | 50 | 0 | -82.7485 | 2.0425 | 2.0425 | 0.00% |
| 2 | 50 | 3.1571 | -77.2803 | 50 | 0 | -82.7485 | 2.8615 | 2.8615 | 0.00% |
| 3 | 50 | 2.8361 | -74.02 | 50 | 0 | -82.7485 | 3.4412 | 3.4412 | 0.00% |
| 4 | 50 | -1.3802 | -84.2814 | 50 | 0 | -82.7485 | 1.0000 | 1.0000 | 0.00% |
| 5 | 50 | -1.1848 | -84.8006 | 50 | 0 | -82.7485 | 1.0000 | 1.0000 | 0.00% |
| 6 | 50 | -0.9009 | -85.5211 | 50 | 0 | -82.7485 | 1.0000 | 1.0000 | 0.00% |
| 7 | 50 | 0 | 0 | 50 | -1 | 2 | 2.3669 | 2.3669 | 0.00% |
| 8 | 50 | -1 | 2 | 50 | 0 | 0 | 2.3669 | 2.3669 | 0.00% |
| 9 | 50 | 2.49 | -0.001 | 50 | -2.49 | 0.0009 | 7.1792 | 7.1792 | 0.00% |
| 10 | 50 | 2.49 | -0.001 | 50 | -2.49 | 0.001 | 7.1792 | 7.1792 | 0.00% |
| 11 | 50 | 2.49 | -0.001 | 50 | -2.49 | 0.0011 | 7.2195 | 7.2195 | 0.00% |
| 12 | 50 | 2.49 | -0.001 | 50 | -2.49 | 0.0012 | 7.2195 | 7.2195 | 0.00% |
| 13 | 50 | -0.001 | 2.49 | 50 | 0.0009 | -2.49 | 4.8045 | 4.8045 | 0.00% |
| 14 | 50 | -0.001 | 2.49 | 50 | 0.001 | -2.49 | 4.8045 | 4.8045 | 0.00% |
| 15 | 50 | -0.001 | 2.49 | 50 | 0.0011 | -2.49 | 4.7461 | 4.7461 | 0.00% |
| 16 | 50 | 2.5 | 0 | 50 | 0 | -2.5 | 4.3065 | 4.3065 | 0.00% |
| 17 | 50 | 2.5 | 0 | 73 | 25 | -18 | 27.1492 | 27.1492 | 0.00% |
| 18 | 50 | 2.5 | 0 | 61 | -5 | 29 | 22.8977 | 22.8977 | 0.00% |
| 19 | 50 | 2.5 | 0 | 56 | -27 | -3 | 31.9030 | 31.9030 | 0.00% |
| 20 | 50 | 2.5 | 0 | 58 | 24 | 15 | 19.4535 | 19.4535 | 0.00% |
| 21 | 50 | 2.5 | 0 | 50 | 3.1736 | 0.5854 | 1.0000 | 1.0000 | 0.00% |
| 22 | 50 | 2.5 | 0 | 50 | 3.2972 | 0 | 1.0000 | 1.0000 | 0.00% |
| 23 | 50 | 2.5 | 0 | 50 | 1.8634 | 0.5757 | 1.0000 | 1.0000 | 0.00% |
| 24 | 50 | 2.5 | 0 | 50 | 3.2592 | 0.335 | 1.0000 | 1.0000 | 0.00% |
| 25 | 60.2574 | -34.0099 | 36.2677 | 60.4626 | -34.1751 | 39.4387 | 1.2644 | 1.2644 | 0.00% |
| 26 | 63.0109 | -31.0961 | -5.8663 | 62.8187 | -29.7946 | -4.0864 | 1.2630 | 1.2630 | 0.00% |
| 27 | 61.2901 | 3.7196 | -5.3901 | 61.4292 | 2.248 | -4.962 | 1.8731 | 1.8731 | 0.00% |
| 28 | 35.0831 | -44.1164 | 3.7933 | 35.0232 | -40.0716 | 1.5901 | 1.8645 | 1.8645 | 0.00% |
| 29 | 22.7233 | 20.0904 | -46.694 | 23.0331 | 14.973 | -42.5619 | 2.0373 | 2.0373 | 0.00% |
| 30 | 36.4612 | 47.858 | 18.3852 | 36.2715 | 50.5065 | 21.2231 | 1.4146 | 1.4146 | 0.00% |
| 31 | 90.8027 | -2.0831 | 1.441 | 91.1528 | -1.6435 | 0.0447 | 1.4441 | 1.4441 | 0.00% |
| 32 | 90.9257 | -0.5406 | -0.9208 | 88.6381 | -0.8985 | -0.7239 | 1.5381 | 1.5381 | 0.00% |
| 33 | 6.7747 | -0.2908 | -2.4247 | 5.8714 | -0.0985 | -2.2286 | 0.6377 | 0.6377 | 0.00% |
| 34 | 2.0776 | 0.0795 | -1.135 | 0.9033 | -0.0636 | -0.5514 | 0.9082 | 0.9082 | 0.00% |
当然と言われてしまいそうですが、ColorACでも論文と一致した結果が得られました。 ColorACに、正しくdE2000が実装されれていると言えそうです。 (勿論結果が一致と言っても、浮動小数点の計算ですから ”表に表示した桁の範囲において一致” です)
このテストデータが入ったColorACのデータファイルを、この章の末尾にリンクした参考データに入れておきます。
重箱の隅をつつく様な話ですが、実はVer0.762までのColorACでは、データNo.14に約0.5%の誤差が発生していました。 ただ以下の説明を読めば分ると思いますが、Ver0.762までのColorACでdE2000の計算をしてしまっていた場合でも 実用上、まず問題無いと思います。
このNo.14のデータ例で誤差が出た理由は、このデータがちょうど分岐点にあたる例になっていて、ColorAC上の演算誤差が元で違う分岐になってしまったため、結果が大きく(と言っても0.5%ですが)ずれていました。
具体的にはCIE dE2000の計算の途中に、計算する色度データを原点から見た角度の差が180度、またはそれよりも小さいと言う条件が出てきます。 ひとつが これです。

No.14のテストデータは 2番目の分岐になる意図の様ですが、Ver0.762までのColorACでは3番目の分岐になってました。 浮動小数点計算の結果が正確に180度差にならず、|h'2-h'1| = 180.00000000000003 となっていました。 180度よりも わずかに大きいだけですが、≦の条件不成立で分岐違いになり%オーダーの差として現れます。
元々、色差を計算するデータが この角度の差が意味を持つほど精度が高い事は ほとんど無いと思いますので、 実用上 まず問題にならないと考えて 放置していました。
今回 この報告で 言い訳を書くよりは 差分を解消できないかと再トライしてみました。結果、角度の差の計算の部分で、計算順を変更して、発生する桁落ちを僅かでも減らす様にする事で、 イコール条件が成立する様になりました。
ColorACは、任意の座標変換が可能であり、色彩輝度計などのXYZの測定値からL*a*b*の色差を計算する用途にも便利に使う事ができます。仮想実験的なデータを元に ColorACによる色差計算の例を作ってみました。
仮想実験の想定は、2つの設定が異なるディスプレイにマクベスチャートの色を表示して、色彩を見比べたと言う状況です。チャートのどの部分が 最も色差が大きく見えるか 計算してみます。
ここで、2つのディスプレイは ひとつは AdobeRGBの標準的なD65に調整したモニタと、 もう一つは 色温度をAdobeRGBを元に7,000K相当に調整したモニタです。輝度は両者共に200cd/m2に合わせて、暗室で測定したものとします。
次の表が、使った階調データと2つのディスプレイの測定値(実際には三刺激値の計算値)、そして 三刺激値を元にColorACで計算したdEとdE2000です。
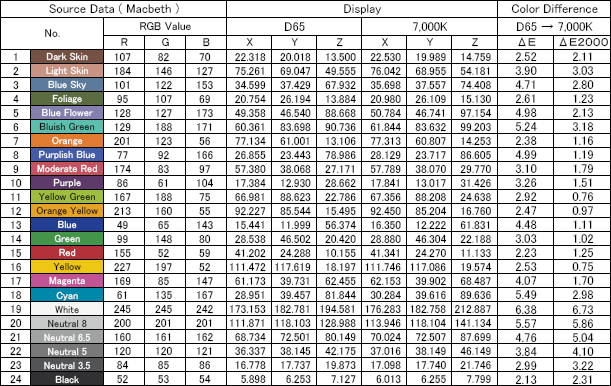
ColorACの表示はこの様になっています(図中の数値はdE2000。計算結果を後からMultipointのOptionとして入力しています。末尾のリンク参照)
やはり無彩色部分の色差が目立つと言う分りやすい結果です。またdE2000を基準に見ると、dEでは黄色、シアンなどの変化を大きく評価しすぎている事が分ります。
多くのディスプレイは発光で色を表現するため、CIELABの本来の想定(光源色を基準のXYZとして用いる)と違っているため、基準のXYZの選択は悩みの種となります。
通常は 対象とするディスプレイの最大輝度の白色を基準のXYZとしますが、今回は2つの 異なる白色のディスプレイがあるため、そのままあてはまりません。
基準の決定には状況設定が必要であり、今回はディスプレイを並べて同時に見ている事を想定しました。 基準は、色度は2つのディスプレイの白色の平均値(三刺激値の平均から計算)で、輝度は基準が2つのディスプレイの三刺激値を下回らない(X/Xn,Y/Yn,Z/Znが100%を超えない)数値を設定してL*a*b*を計算しています。
上の計算の値検証と、下のディスプレイ色温度の色差計算のColorACデータを掲載します。値の検証はCIEL*a*b*の値を直接入力して計算する例として、またMacbeth色彩の例は三刺激値XYZの値を入れて計算する例です。
ColorACには色温度(相関色温度)の計算が実装されています。
ColorACにおける相関色温度の計算方法は、ColorACの説明書"ColorAC_doc2.pdfの4-5,4-6に記載の通りで、 素直にプランクの放射式から求めています。面白味はありませんが、正確な結果が期待できます。
今回 JS Z 8725に準拠した計算(付表と補間に基く計算)もサポートしようと考え、JIS Z 8725:1999の内容を再確認すると共に、 ColorACの計算結果と比較したので報告します。
注: 以下 ”ColorACの計算”との記載は 従来からColorACに実装していた計算方法を指します
注: 以下 JIS Z 8725 との記載は JIS Z 8725:1999を指します
日本では、相関色温度を規定するものとしてJIS Z 8725:1999(光源の分布温度及び色温度・相関色温度の測定方法)が良く参照されています。 JIS Z 8725は色温度についての定義、計算、測定の方法について整理、規定したもので、1999年に改定されたものが現行の規格です。
このJIS Z 8725の色温度(相関色温度)の定義は 一般的な(たとえば ColorACの説明書 に記載されている様な)説明と同じで特別なものではありません。 JIS Z 8725の”附属書2(参考) 相関色温度の計算方法”に 次の様に端的に規定されています。
その光源の u v 色度座標にもっとも近い色度座標をもつ黒体放射の絶対温度として定義される。
相関色温度の定義として、理想的な黒体(プランクの式)ではない放射を想定するものもある様ですが、このJISの定義は黒体が基準であり、プランクの放射の式からスペクトルが計算できます。
この概念的な相関色温度の定義だけでは、 計算する人により 適用する定数の選び方や計算精度などが違ってきてしまうので、 JIS Z 8725では
5. 相関色温度又は色温度の測定方法
で 付表1(または付表2)を用いて相関色温度を求める方法が指定されています。 また付表の使いたについても附属書2(参考)
相関色温度の計算方法
に具体的なプログラム例が記載されています。
この参考プログラムと同等の内容のアルゴリズムで計算する事と、テーブルデータとして指定の付表を適用する事の2つを満たせば JIS Z 8725に準拠した相関色温度の計算と言えそうです。
もともとColorACに実装していた相関色温度の計算も、概念的な定義は JIS Z 8725の考え方と同じです。
具体的な計算の方法としては、予め黒体放射軌跡のデータをテーブルとして保持するJIS Z 8725の手法とは違い、 ColorACでは直接プランクの式から黒体放射スペクトルを求めて、色度を計算します。C++による倍精度の浮動小数点計算です。 相関色温度は、繰り返し色度点と黒体放射軌跡の距離を計算して一番近い黒体放射曲線上の点の色温度として求めています。
この相関色温度の定義そのままの計算を実施しようとすると、まず問題になるのが プランクの式に適用する物理定数の値です。 プランクの式ではプランク定数、ボルツマン定数 および光速の組み合わせから作られるc2(放射の第二定数)の値を決める必要があります。 起源の古い規格等は、古い異なる定数値を使って作られているので、比較には注意が必要です。
現在は、物理定数はCODATAの推奨値を用いるのが一般的です。 JIS Z 8725の中では このc2の値は桁を
まるめて記載されていて、どの数字を想定していたのかは分りません。
| CODATA1986 | 0.01438769 |
| CODATA1998 | 0.014387752 |
| CODATA2010 | 0.014387770 |
| JIS Z 8725 | 0.014388 |
JIS Z 8725 がこの数値を使う理由は知りませんが、この数字が国際的にも標準として使われている規格の様です。 従来 ColorACではCODATA1986の値を使っていましたが、JIS Z 8725 に合わせて 0.01438800を使う事にしました。 (ColorAC Ver0.762から変更。以下の計算例はこの条件です)
ColorACでの色度点と黒体放射軌跡の距離の求め方ですが、相関色温度を求める対象のCIE1960の色度u,vに対して、 温度Tcの黒体の色度のCIE1960表現を、uBL(Tc),vBL(Tc)とおいたとき、 両者の幾何学距離の2乗 D2BLは、
D2BL(Tc) = ( uBL(Tc) - u )2 + ( vBL(Tc) - v )2
となります。
このD2BL(Tc)を用いて、相関色温度を求める計算は、 充分小さいΔTに対して、次の2つの式の条件を満たすTcを見つける問題
と表現できます。
この時、相関色温度Tcpは、およそ±ΔT程度に求められた とみなす事ができます。
このΔTは上記の式を確認しながら繰り返し計算して、徐々に小さくして行きます。この 繰り返し計算の収束(十分ΔTが小さくなった)は、上記の式が成立している限り、試行刻み幅=ΔT≦Tc/108まで実施するので、 相関色温度の数値として有効桁5~6桁を想定する場合、収束に関しては十分(すぎるぐらい)と言えます。
ただ偏差duvが大きい場合には色温度と距離の関係が緩慢になる(たとえば計算結果が D2BL(Tc) = D2BL(Tc+ΔT)になるなど) ため、 目標のΔT≦Tc/108の前に計算を打ち切る必要が出てきます。
そこで、実際に相関色温度を計算した時に、どこまでΔTを小さくできているか調査しました。 乱数でu=0.595~0.0825、v= 0.3885~0.2395の範囲に乱数で色度点を発生させて相関色温度を計算し、計算結果に適用されたΔTの最大(最悪)値を確認します。色温度やduvにより精度が変わると考えられるので、段階に分けて集計しました。下表がその結果です(試行回数は全体で 107回)
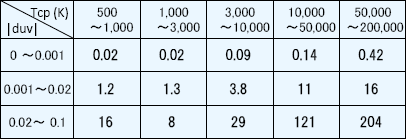 ΔTの最大(最悪)値
ΔTの最大(最悪)値
(Tcpに対する割合 ppm)
結果は予想通り、duvが大きいほど、また色温度が高いほど誤差が増える傾向になりました。 最も悪い値でも204ppm(0.02%)となっていて、実用上問題無い精度と言えると思います。
また、|duv|<0.02(JIS Z 8725によれば、Tcを相関色温度と呼べる範囲)に限れば、最大で16ppm=0.0016%と、十分高精度になっていました。
相関色温度の計算が正しいかどうか(精度ではなく確度)の確認のために、信頼できる色度座標と相関色温度がセットになったデータが欲しい所です。探したのですが、色度座標の有効桁が少なかったり、信頼できる文書でなかったりで、都合の良いデータはなかなか見つかりません。
見つけた中では良さそうなデータと比較の結果を一つ提示します。
CORM 2011の "Calculation of CCT and Duv and Practical Conversion Formulae"の中に、 相関色温度2,900K duv=0.02の色度(真値)から、相関色温度を誤差0.006Kまで求める例があり、文献上読み取れる色度数字は (u,v)=(0.247629,0.367808)となっています。 (表示はExcelのスクリーンショットの様で、もっと桁が多いはずですが 見えません)。
この色度をColorACで計算すると 2900.0086・・・K、duv=0.020000・・・となります。元の色度の桁が足らない可能性があるので、 最後の桁の下の桁に±5の範囲の数字があると考えて3x3のデータ点を作ってした結果が以下です。
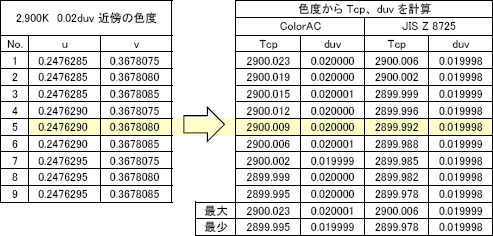
やはり小数7ケタ目の数字で相関色温度の0.01K台の数字が変わっていて元の色度値の有効桁不足が示唆されていますが、 ColorACおよびJIS Z 8725共に
0.1K程度まで正しい数字になっています。
さらに、ColorACおよびJIS Z 8725の精度を確認するためには複数の相関色温度の有効桁数が多い色度データが必要ですが無いので、 Microsoft Excelでプランクの式から色度を計算し、 その色度から複数の手段で色温度を計算して比較しました。
色温度からの色度計算は、プランクの式でスペクトルを求め、CIEの等色関数(数表)を 使って、色度に変換したものです。Microsoft Excelのスプレッドシート上でマクロ等を使わず簡単に計算できます。 これを プランクの式から求められる色度の正しい計算結果として使えると考えます。
c2(放射の第二定数)の値はJIS Z 8725と同じ数値を用いています。 色温度は、一番下のデータを除き、JIS Z 8725の付表のデータ点から選んであり、 JIS Z 8725でも 補間の誤差はほとんど出ない色度座標になっています。
一番下のデータは、他のデータが 10進数でちょうどきりの良い数字であるため、特殊な数字のみの検証と誤解されない様に、中途半端な数値を入れてみました。
比較対象は ColorAC、JIS Z 8725、 Lindbloom.comのCIE Color Calculator、およびMcCamyの近似式です。
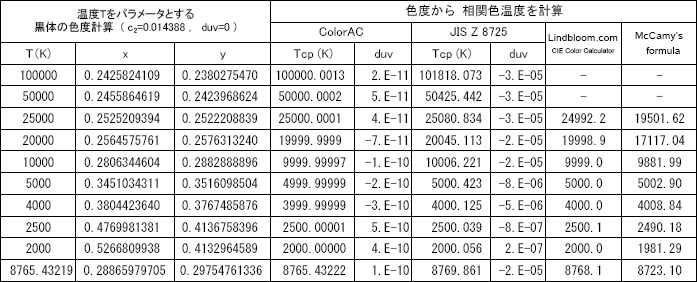
ColorACについては、元にしたデータがduv=0であるため精度低下要因が無く、上述した様に1/108までの収束計算を反映した精度が得られています。
また、Lindbloom.comのサイトのCIE Color Calculatorも、精度良く再現できています。 プランクの式から求めた色度と、ColorAC、Lindbloom.comの3者は一致すると言ってよいと思います。
また、JIS Z 8725 については、高温側で誤差が目立ちますが、基本的にはプランクの式から求めた色度と合致していると考えてよいと思います。
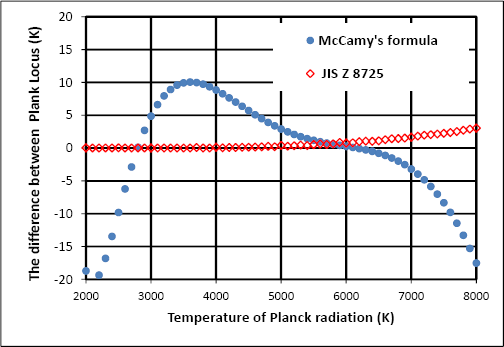
McCamyの近似式は、高精度との情報(直接McCamyの論文を確認していませんが、2,856Kから6,500Kが、2K以下の確度で計算できる) があり、信頼性の高い数字が得られる手段と考えて加えたのですが、予想外に誤差が大きいと言う結果です。
脱線しますが、McCamyの近似式の誤差ΔTを 2000Kから7000Kの範囲でプロットしてみて、精度が良いとの話の意味がわかりました。 McCamyの近似式が2K以内の高精度とは、色温度が2,856K(A光源)と6,500K(D65光源)の付近 ただ2点に着目しての話しの様です。
私が Webで公開されているJIS Z 8725のテキストを見て気づいた点、及び計算を確認した結果見えてきた問題に以下があります。
| (1) 2度視野の付表のvの値のに誤記がある | → | JIS Z 8725 H17年に修正済み |
| (2) 2度視野の付表のuの値に2ヵ所誤記がある | → | JIS Z 8725 H21年に修正済み |
| (3) プログラム例のコードに誤記があり、計算できない | → | 部分的に修正済み(いつ?) |
| (4) 10度視野の付表にも誤記らしき部分あり | → | 修正されていない |
| (5) 高温になるに従いColorACの結果とずれてくる | → | ColorAC側のバグ? |
現在Web上で見られるJIS Z 8725のテキストでは、参考プログラムの問題(3)、付表の数字の誤記(2) が適用されていないため そのままでは使えません。
今回 この問題点についてレポートしようと思ったのですが、 JIS Z 8725を購入して確認したところ、 上記の様に(1),(2)は訂正済み、(3)も 実行して答えが返る程度には修正されている事が分りました。
Webから参照できるJIS Z 8725のテキストでは、条件付きループ(DO LOOP UNTIL)を抜ける判断が DT!(j)=0 となっていて、偶然この条件が成立する入力値を与えた場合以外は正しく動作しません。
テーブルの補完のためにはDT!(j)>=0の条件、および添え字jは j-2が以降に参照されるため j-2>0の条件が必要です。
現在発行されているJIS Z 8725ではDT!(j)>=0の条件に修正されていますが、色温度の高い領域では j<=2でループから抜けてしまうため、 jの添え字範囲のケアが必要です。
色度(u,v)を与えて相関色温度を計算し結果について、ColorACとJIS Z 8725で比較してみました。
計算ポイントは およそ 1,500K~35,000Kの±0.035duvの範囲で、u,v上0.005きざみで 等間隔に500点選びました。
まず10度視野(CIE1964)の計算から先に比較結果を示します。
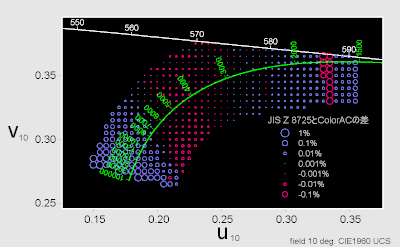 JIS Z 8725で求めた相関色温度Tcs1と
JIS Z 8725で求めた相関色温度Tcs1と
ColorACの計算による相関色温度Tcs2の
差 (Tcs1-Tcs2)/Tcs2 (10度視野)
図上の○の大きさが ColorACとJIS Z 8725差を示します。
相関色温度が1,750K近辺で局所的に差が大きくなっていますが、 そこを除くと全般に0.3%以下、10,000K以下に限れば ほぼ0.01%以下の差となります。 両者は良く一致していると言えると思います。
相関色温度1,750K近辺の差ですが、JIS Z 8725 の付表を確認すると、 1/Tcp = 580のuの値 0.330 611 が前後のuの値に対してずれています。 この値を前後のuの値から補間して たとえば 0.332 559 を入れると 次の図の様に1,750K近辺での差の局所増が無くなります。 ただ 残念ながらこの修正をしてしまうとJIS Z 8725に準拠しない結果と言う事になります。
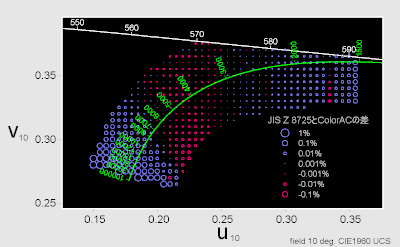 10度視野付表のuの値を修正して
10度視野付表のuの値を修正して
求めた相関色温度Tcs1と
ColorACの計算による相関色温度Tcs2の差
(Tcs1-Tcs2)/Tcs2)
前節の10度視野と同様に2度視野の計算結果を比較したのが下図です。
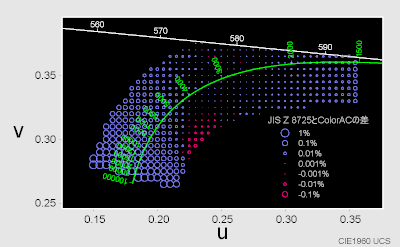 JIS Z 8725で求めた相関色温度Tcs1と
JIS Z 8725で求めた相関色温度Tcs1と
ColorACの計算による相関色温度Tcs2の
差 (Tcs1-Tcs2)/Tcs2 (2度視野)
ただ、全般に色温度が高い方向にずれていて、特に高温側で 差が大きくなる傾向あります。この高温側で差が増える傾向は10度視野でもあったのですが、2度視野ではより目立ちます。 10,000Kあたりでも誤差が増えていますが、10,000KはJIS Z 8725で使うデータテーブルの中央付近にあり、補間の誤差の傾向とは考えられません。
付表のテーブルデータ値を確認すると、テーブルデータのuvの座標値自体が プランクの式から計算した黒体の色度からずれている事が分りました。 この差がColorACの計算結果との差になって見えている様です。
この差が何に由来するものなのか、現時点良く分かりません。プランクの式になんらかの補正項を加えているのか、あるいは単にデータを作った当時の計算精度が悪かっただけなのか・・・
HSVは、RGB色空間の変換として式が定義されています。その定義式ではYMCの部分も最大(たとえばYならばRGB=(255,255,0) )となります。 従って、やはりスジ状に見えます。 これはxy色度図の様に、輝度を調整すべきか、それとも変換式をRGBの強度=画像の画素データと考えて補正しないのか、どちらが正しいのでしょうか? いま良く判らず、まずは変換式から単純に描画(補正無し)としています。 (3D表示であれば、当然V方向の情報として正しく表現できるので悩む必要が無いのかも)
→ HSVの場合はデータ空間と考えて補正無しが正しいですね。
トップに戻る
LABは大変苦労しているのですが、より軽微な問題として、xy色度図などでも考えるべき点があります。 xy色度では、座標で色は決まるのですが、輝度をどうするかは色度図を作る側の検討項目となります。
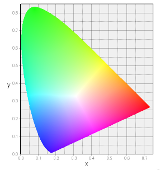
この図は、インターネット上の色度図など、電子データの色度図で良く見る ある特徴 があります。 それは、RGBの3原色が混色するYMCの部分が輝いてスジ状に目立って見えている事です。
実は、この図は色データとしてRGBの階調のどれかが最大の階調(256階調だと値255)になるルールで描画しています。 混色の部分は単色のRGBよりも当然、加法混色して輝度が大きくなるので、当然スジ状に目立って見えてきます。
これは、画像の表現がRGBを原色としたシステムだから見える、ディスプレイの方式特有の現象であり、 色度図の本質とは何ら関係無いので、色度図としては好ましくない不自然な見栄えだと言えます。
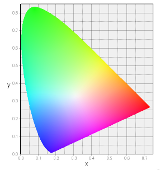
ColorACの色度図はそうならない様に混色部分の輝度を下げる様に調整しています。 (それでも、表示/印刷のガンマ値が想定と違うと、輝度分布が崩れてRGB混色の欠点が露呈して、やはりスジ状に見えてしまう場合があります)
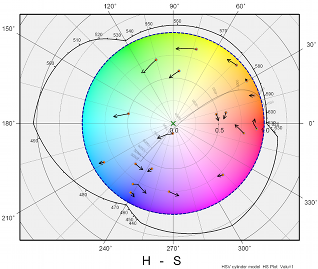
さて一方HSVは、RGBの3原色が前提の表現で、変換式も明確に決まっている表現方法であるため、RGBの3原色を決定すれば 三刺激値データ(あるいは色度+輝度など)とHSVの変換式が決まります。
試しに3原色をsRGBとして描画してみたのがこの図です。
単波長軌跡、黒体放射軌跡がHSV上でどうなっているかが分かります。
L*a*b*から、a*,b*の色度図の作成を考えます。
ColorACにa*-b*色度図の描画機能を実装しようとしたら、a*-b*面での描画色は、一意に決定できない問題である事に気付きました。
xy色度図ではPCモニタ上で表示できる色と色度図の色の差分をどう処理するかに工夫が必要でしたが、もっとずっと深刻な問題です。 L*a*b*では、ある a*,b*の座標における色そのものが、L*の取り方で変わってしまうため、一般論としては、色を決められません。
適切な前提条件を付加する必要がありますが、一般的に適切と言える条件を作るのは難問です。
たとえば、波長軌跡(Spectrum Locus)を描画しようとする場合、輝度の情報は無いので、L*を決定するルール(条件)を置かないといけません。
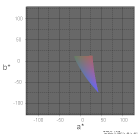
一番単純な方法として、L*をある値に固定してしまって、a*,b*の断面を描画する事が考えられます。やってみました。
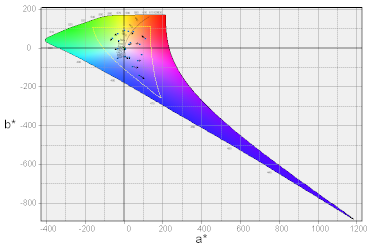
右図はL*a*b*における基準の三刺激値をD65光源とし、L*=100で固定して波長軌跡を描画したものです。 見ての通り、短波長側(青側)が すごく伸びた形状になっています。これは短波長側で視感度が低下するにも関わらず、
L*=100と不自然に固定してしまったために、それを反映して伸びたものと考えられます。
この図は定義が明確であり、十分意味のある図と考えますが、a*-b*の色のイメージとして汎用なものが欲しい所です。
※この短波長部の長く伸びた部分は、パワーが急上昇している状態(視感度が低下するのにL*は一定)であり、不自然、かつ図としてもモニタや印刷では それを表現できません。
では、L*を小さい値に設定すれば良いかと言うと、この傾向は変わらず解決にはなりません。
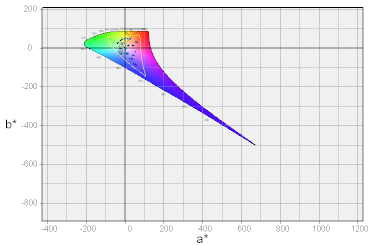
結局、視感度の悪い波長部分でも、L*が保たれてしまう事が不自然になる根本原因です。実際の評価対象の色のバリエーションと同じ様なL*の振る舞いをするモデルが必要です。
そこで、ディスプレイを模してRGBの3原色を仮定し、その組み合わせで明度L*を決めれば 自然な形状になるのではないかとと考えて 作ってみました。
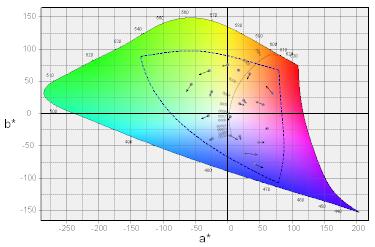
青の異常な広がりは無くなって目論見通りにはなりました。 しかし、RGBの3原色をどう設定するのか根拠ある方法なのかについて、良いアイディアが浮かびません。
表示するデータが、RGB3原色のディスプレイ画面の色度などであれば、測定するディスプレイの原色RGBと 計算の原色RGBを一致させる事でうまくいくのかも...しかし、これでは3原色のシステムにしか適用できません。
今、別の考えとして波長ごとの視感度の値をL*に変換して描画すれば、もう少し自然で適切な図が作れないかトライ中です。
この考え方だと、一定のエネルギーのa*,b*をプロットする事になりますが、逆に たとえば短波長側で視感度がゼロに漸近するとL*=0 すなわちa*,b*もゼロとなり、不自然な図になる事が予想できます
とにかくL*a*b*を2Dの色度図として成立させる事が結構難しい事は分かりました。
素直に、3Dグラフとして描画した方が、ずっと簡単だと思えます。
元々、ColorACはxy色度図を描画する事をメイン機能として作っているソフトです。 xy色度図は2次元データですので、そのまま2次元のグラフとして表現可能です。
しかし、明るさの情報を含んだ3Dの表現としてL*a*b*(CIELAB)や、HSV色空間なども良く使われています。
ColorACでも、これらを表示する事を考えました。図として3Dにしてしまうと、変更が大きすぎるので、 まずは2Dの図としての描画を考えました。
L*a*b*で、L*(明度Lightness)は明るさを、a*,b*が色を示すのでこのa*,b*を2次元グラフとして作図すれば、 xy色度図と同様な図がなりそうです。実際に、その様な図が世の中にあります。
ColorACでも、XYZ三刺激値のデータなどから、多少の座標変換によってa*,b*色度図を表示するのは たやすい事に思えました。 ColorACの変更点は、座標変換関数を追加する事と、入力データとして3次元のデータに対応する事が主となるでしょう。
HSVについても、同様にHとSの平面を取り出せば、2次元になり、 直交座標に変換すれば、xy色度図と共通の描画ルーチンが使えるでしょう。
色度データで、色度のばらつきなどのデータをプロットしようとすると、沢山のx,y値を入力、編集する必要があります。
この処理は、Excelなどの計算表のイメージの編集環境を思い浮かべて、それを実現しようと考えました。
MFCを使っているので、ちょうど良さそうなCListCtrlクラスがあります。これで簡単に実現できる思ったのですが、そのままでは使い物にならない事が判明。
データセルをクリックしての編集だけでも、CListCtrlでの実現は設定が難しそうでした。
CListCtrlクラスのオーバライドは、手に余りそうだったので、データ入力の時だけ、他の手段で実現できないか考えました。 クリックした数値の位置に、別に非表示にして準備しておいたCEditをMoveして表示して、そのCEditに編集をやらせれば良いと考えたのですが、 実際作って見ると、CEditからデータを取り出した後の動作の調整などが、なかなか難しい。
一旦諦めて、他の人がどんな方法で実現しているか検索してみました。 すると、このCEditをCListCtrlの上に重ねる方法での実現を薦める意見がいくつもヒットしました。
やり方は間違っていないと、自信が持てたので、諦めずカットアンドトライの繰り返し...。
まだ多少操作に対して不安定な感じもするのですが、CRやTABキーで次のセルに編集が移るところなど、最初のイメージに近いものが作れたと思います。
色度について御存知の方は、コンピュータの画面(モニタ)に 正しい色度図を表示する事が実際には不可能です。 モニタの表示できる色度範囲が、色度図全体を表示するには足らないからです。正しい色の色度図は作れません。従って、色度図を作ろうとしたら、どうやって本物らしく見える色度図を作るかが課題となります。
いきなり 作る目的が正しい色度図では無いと言う話になりましたが、現実に色度図を描こうとしたら、この本物っぽさが重要です。
基本的には、色度図全体の色を淡するか、または出ない濃い色の部分をうまくグラデーションを付けて、モニタで表示できる色度範囲で表示しても不自然に見えない様にします。
しかし、この考えだけで作ってみると、 書籍等に掲載されている色度図とはだいぶ違うものが出来上がります。書籍は印刷で白つぶれているためか、白色部分がはっきりと白く見える場合が多いです。 正しい、白く見えない色度図がいいのか、あるいは正しくはないが、白色部分が白く見える色度図が良いのか。
また、色度図の使い方として、色を塗った部分(何と呼ぶのが適切か、この部分を特定する呼び方が判らないのですが・・・とりあえず可視領域彩色とでも呼びます)の 上に、測定した色度のマークを表示したり、重ねて使う事になりますが、正しい色度図だと、マークが見え辛くなったりします。 そんな場合は、あえて正しくない事は承知して 色を淡くしたくなります。
そこでColorACでは、単純にRGBの色をミックスして色度図の座標に相当する色を作るだけでなく、白色付近をより白っぽく脚色したり、 色の濃さを調整できる様にしました。
ColorACでは、色度図を画像ファイルとして出力します。 使い方としては画像ファイルをパワーポイントに貼ってプレゼンで使ったりする事を想定していますが、 画面に表示、印刷するなど、モニタやプリンタで色の再現性がバラバラなので、この調整機構は
最終出力装置(プリンタとか)での見栄えを改善する目的でも使えると思います。
ソフトを開発しようとすると、一般素人としては、情報が手に入りやすいWindowsか、Linux系かMacのどれか。 私は仕事でもWindowsを使っていて、いちばん慣れているWindowsで開発する事にしました。 ソフトの仕様の大枠は、以下の様に考えました。
・ソフトが出力する色度図の内容としては、資料として完成された色度図を作りあげるのは、あまりにもやる事が多すぎるので、 他の資料作成に使うソフトに貼り付けて仕上げる事を想定して、必要最低限の部分(色度図)を作る事にしてハードルを下げる。
・Windowsの業務ドキュメントを作る環境としては、MS-Officeがデファクトスタンダードなので、 それらで読み込めるデータ形式のファイルを出力する必要がある。 再編集の可能な拡張メタファイルが魅力的だったのですが、しかしそれでは本当にWindows限定になってしまう。 ソフトはWindowsでしか動かないけど、成果物は汎用性をもたせたい。 結局一番簡単で使いまわしが効く画像ファイルで出力するコンセプトで。
グラフ作成ソフトなので、操作性が重要です。 色度図を描くだけのために使い辛いソフトを使うぐらいならば、Excelで三角形のおむすび型の輪郭だけ描くだけで十分て人が多そうです。
いくらフリーソフトでも、一定レベル以上の作り込みで使い勝手を良くしなければ使ってもらえない。今回は、使い勝手にも力を入れて作っています。